The Tower of Hanoi problem.

고전적인 하노이타워 문제변형을 풀어봤다.

 

기존 하노이타워 문제는 3개의 rod와 여러개의 disk가 존재하는데, 1rod에 존재하는 모든 disk를 3rod에 모두 옮기면 되는 문제이다. 단, disk의 크기는 모두 다르고, disk는 한번에 한 개씩 옮길 수 있으며,  큰 disk가 작은 disk 위에 올라가서는 안된다. 라는 조건이 들어가 있다.

 

위 문제의 코드를 작성하면,

 

hanoi1

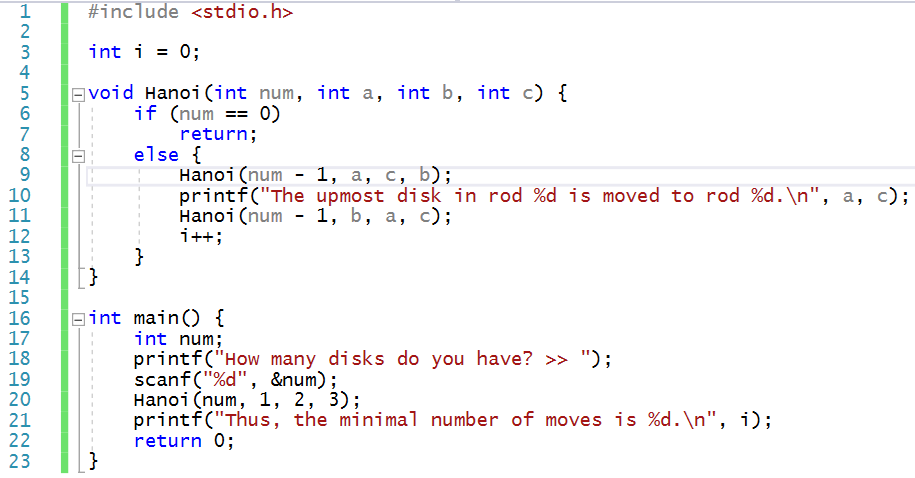
이렇게 작성할 수 있다.

 

honoi는 재귀함수 방식을 쓰며, 해당 코드를 분석하면

#9 rod1에 있는 n-1개의 disk를 rod2에 옮긴다.

#10 rod1에 있는 마지막 disk를 rod3에 옮긴다.

#11 rod2에 있는 n-1개의 disk를 rod3에 옮긴다.

 

해당 코드의 출력값을 보면

hanoi1_1

hanoi_3

이렇게 출력이 가능하다.

 

그럼 이제 하노이타워 변형문제에 대해 설명하겠다.

이번 문제는 disk를 옮길때 rod를 건너 뛸 수 없다는 조건이 들어간다. 말 그대로 rod1에서 rod3으로 옮기고 싶다면 반드시 "rod1에서 rod2", "rod2에서 rod3"이렇게 두번 출력해주어야 한다는 말이다.

 

해당 문제를 코드로 작성하면

 

hanoi2

이런식으로 작성할 수 있다.

 

해당코드를 분석하면

#10 rod1에 있는 n-1개의 disk를 rod3에 옮긴다.

#11 rod1에 있는 마지막 disk를 rod2에 옮긴다.

#12 rod3에 있는 n-1개의 disk를 rod1에 옮긴다.

#13 rod2에 있는 마지막 disk를 rod3에 옮긴다.

#14 rod1에 있는 n-1개의 disk를 rod3에 옮긴다.

 

해당 코드의 출력값을 보면

hanoi2_1

hano2_3

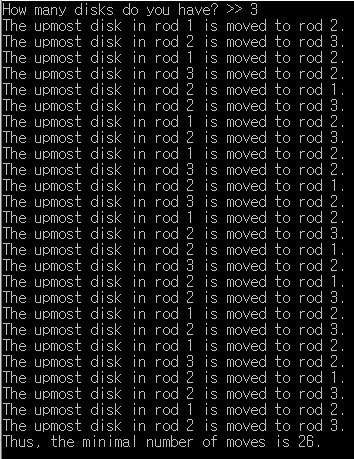
출력 마지막 부분을 보면 이동한 횟수가 나오는데, 해당 코드는 𝑇𝑛 = 3𝑇(𝑛−1) + 2 그리고 𝑇1 = 2. 를 따른다.

해당 수열을 정리하면,  이동한 최소 횟수는 𝑇𝑛 = 3^𝑛 − 1 를 따르는 것을 알 수 있다.